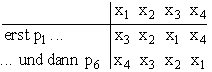Die Ideen der Galois-Theorie
Jörg Bewersdorff
 Wohl selten war eine wissenschaftliche
Entdeckung von so dramatischen Umständen begleitet wie die des
erst zwanzigjährigen Mathematikers Evariste Galois. Mit einem in
der Nacht zum 30. Mai 1832 verfassten Brief übersendet Galois
einem Freund Manuskripte, die seine Forschungsergebnisse der
vorangegangenen Monate beinhalten. Am nächsten Morgen stellt
sich Galois einem vereinbarten Duell, wird dabei schwer verwundet
und stirbt am Tag darauf.
Wohl selten war eine wissenschaftliche
Entdeckung von so dramatischen Umständen begleitet wie die des
erst zwanzigjährigen Mathematikers Evariste Galois. Mit einem in
der Nacht zum 30. Mai 1832 verfassten Brief übersendet Galois
einem Freund Manuskripte, die seine Forschungsergebnisse der
vorangegangenen Monate beinhalten. Am nächsten Morgen stellt
sich Galois einem vereinbarten Duell, wird dabei schwer verwundet
und stirbt am Tag darauf.
Galois Entdeckungen, ihm zum Ehren später Galois-Theorie genannt, lösen eine Fragestellung der Algebra: Unter welchen Bedingungen ist eine Gleichung in einer Unbekannten auflösbar? Noch wichtiger als das gelöste Problem ist allerdings die von Galois dazu verwendete Methode. Ihre Inhalte, namentlich der Begriff der Gruppe, aber auch die Vorgehensweise, unterschiedliche Typen von mathematischen Objekten geschickt miteinander zu verknüpfen, sind heute zum unverzichtbaren Bestandteil der Mathematik geworden.
Die Darstellung der Galois-Theorie erfolgt in modernen Lehrbüchern meist sehr abstrakt. Im Sinne der universellen Bedeutung ist dies zweifellos unabdingbar. Leider wird aber dem mathematischen Laien dadurch der Blick auf die wesentlichen Ideen Galois versperrt. Dem soll hier, wenn auch im bescheidenen Rahmen, abgeholfen werden.
Das Problem
Ausgangspunkt für Galois war das damals ungelöste Problem, dass die Lösung von Gleichungen in einer Unbekannten wie etwa
x2 - 2x - 4 = 0
oder
x3 - 3x2 - 3x - 1 = 0
betrifft.
Seit dem 16. Jahrhundert sind für solche Gleichungen allgemeine (Auf-)Lösungsformeln bekannt, solange der Grad, also die höchste Potenz der Unbekannten x, nicht größer als 4 ist. Mit den Lösungsformeln können die Lösungen ausgehend von den Koeffizienten, also den Konstanten der Gleichung, durch endlich viele Rechenschritte bestimmt werden. Dabei werden – und das ist die wesentliche Eigenschaft – neben den vier Grundrechenarten nur Wurzeloperationen benötigt. Verwendet man die Lösungsformeln bei den beiden oben angeführten Gleichungen, erhält man
![]()
als eine Lösung der ersten Gleichung sowie
![]()
für die zweite Gleichung.
Beide Gleichungen besitzen noch weitere Lösungen. 1799 bewies der damals 22-jährige Carl Friedrich Gauß, dass eine Gleichung n-ten Grades n Lösungen besitzt. Allerdings bedarf diese Aussage einer Kommentierung: Kann beispielsweise eine Gleichung dritten Grades in eine Form der Gestalt
(x - x1)(x - x2)(x - x3) = 0
umgewandelt werden, dann sind offensichtlich die Zahlen x1, x2 und x3 die Lösungen der Gleichung – und keine anderen Zahlen sonst. Zu einer Gleichung n-ten Grades kann man immer, so der von Gauß bewiesene Satz, n Zahlen x1, x2, ..., xn finden, so dass die Gleichung entsprechend zerlegt werden kann. Damit besitzt eine Gleichung n-ten Grades stets n Lösungen.
Allerdings müssen die Lösungen nicht unbedingt reell sein, also einer auf dem Zahlenstrahl lokalisierbaren und damit real vorstellbaren Größe entsprechen. Möglich sind vielmehr auch Lösungen im Bereich der komplexen Zahlen, das sind Zahlen der Form a + bi, wobei die Zahl i die Eigenschaft einer Quadratwurzel von -1 besitzt: i·i = -1. Außerdem kann es durchaus vorkommen, dass einige der Lösungen x1, x2, ... übereinstimmen; auf solche Gleichungen wollen wir hier nicht eingehen – es wird lediglich angemerkt, dass ihre Auflösung auf den Fall mit lauter verschiedenen Lösungen zurückgeführt werden kann.
Der von Gauß bewiesene Satz ist eine reine Existenzaussage – über konkrete Werte der Lösungen oder Verfahren, wie sie berechnet werden, sagt er nichts aus.
Nachdem hunderte von Jahren alle Versuche, eine allgemeine Lösungsformel für die Gleichung fünften Grades zu finden, gescheitert waren, begannen sich zum Ende des 18. Jahrhunderts Zweifel auszubreiten, ob eine solche Formel auf der Basis von Wurzelausdrücken überhaupt existiert. Ein insgesamt schlüssiger Beweis dieser Vermutung gelang aber erst 1824 dem norwegischen Mathematiker Niels Henrik Abel.
Damit war klar, dass es keine Formel gibt, die zu jeder Gleichung die Lösungen in Form von Wurzelausdrücken angibt. Wie sieht es aber für spezielle Gleichungen aus, wie zum Beispiel
x5 + 15x - 44 = 0
oder
x5 - x - 1 = 0.
Sind diese beiden Gleichungen fünften Grades auflösbar, das heißt, gibt es Wurzelausdrücke für sämtliche Lösungen oder nicht? Galois Ergebnisse ermöglichen eine Antwort: Nur die erste Gleichung ist auflösbar, beispielsweise ist
![]()
eine Lösung, wohingegen die Lösungen der zweiten Gleichung nicht derart durch Wurzeln darstellbar sind!
Zu betonen ist, dass Wurzelausdrücke für die Lösungen nicht deshalb gesucht werden, um numerische Werte zu berechnen. Das Interesse an ihnen resultiert ausschließlich aus grundsätzlichen Erwägungen heraus – vergleichbar etwa mit Dreieckskonstruktionen in der Geometrie, wo auch dem "ob" und "wie" mehr Gewicht als dem konkreten Resultat zugemessen wird.
Dagegen reicht es bei praktischen Anwendungen, wenn die numerischen Werte der Lösungen berechnet werden, etwa (in willkürlich gewählter Reihenfolge)
x1 = 4,51521655..., x2 = 0,84506656..., x3 = 0,31321057..., x4 = -1,67349369...,
wenn die Gleichung
x4 - 4x3 - 4x2 + 8x - 2 = 0
zu lösen ist.
Numerische Resultate können mit einer Vielzahl von effektiven Näherungsverfahren bestimmt werden. Die meisten von ihnen arbeiten iterativ, das heißt, sie liefern schrittweise immer genauere Werte. Ist die gewünschte Genauigkeit erreicht, wird das Verfahren abgebrochen. Wurzelausdrücke für die Lösungen lassen sich aus rein numerischen Ergebnissen allerdings kaum ableiten.
Die Galois-Gruppe einer Gleichung
Die Vorgehensweise von Galois ist für die heutige Mathematik sehr typisch, zu seiner Zeit war sie gewiss revolutionär: Jeder Gleichung wird ein Objekt zugeordnet, heute Galois-Gruppe genannt, dessen Eigenschaften Aufschluss darüber geben, ob die Gleichung auflösbar ist oder nicht.
Konstruiert wird die Galois-Gruppe mit Hilfe von (Rechen-)Ausdrücken wie
x1 + x2 x2 - x2 x3,
die sich aus den Lösungen x1, x2, ... mittels der Grundrechenarten bilden lassen. Auch ohne Kenntnis der Lösungen ist es häufig möglich, die Werte solcher Ausdrücke zu bestimmen. So ist die Summe aller Lösungen immer gleich dem mit -1 multiplizierten Koeffizienten der zweithöchsten x-Potenz. Beispielsweise für die genannte Gleichung vierten Grades gilt
x1 + x2 + x3 + x4 = 4.
Bei derselben Gleichung ebenfalls leicht bestimmbar sind
x1 x3 + x2 x4 = 0
und
(x2 + x4 + x1 x2 x3 x4)2 = 8.
Etwas aufwendiger darzustellen sind die Werte der folgenden Ausdrücke:

Genau zu beschreiben, wie man solche Identitäten findet, würde hier zu weit führen. Nur soviel: Man ist keineswegs darauf angewiesen, die Gleichungen mit Hilfe der numerischen Werte nachzuprüfen, soweit dies aufgrund der nie ganz vermeidbaren Rundungsfehler überhaupt möglich ist. Vielmehr ist jeder dieser Ausdrücke Lösung einer Gleichung, die aus der Ausgangsgleichung bestimmt werden kann und zwar mit allgemeinen Formeln, die nur Grundoperationen enthalten. So ist etwa der Ausdruck x1x3 + x2x4 für alle Gleichungen vierten Grades Lösung einer Gleichung dritten Grades, die eine Berechnung des Wertes ermöglicht. Im hier gewählten Beispiel geht dies bemerkenswert einfach, man erhält den Wert 0.
Hingegen sind für andere Gleichungen vierten Grades meist umfangreiche Wurzeloperationen notwendig, um die Werte der genannten Ausdrücke darzustellen. So gesehen, spiegeln diese Identitäten Beziehungen zwischen den Lösungen wider, die auf eine gegenüber dem allgemeinen Fall verminderte Komplexität schließen lassen. Galois Verdienst ist es nun, solche Sachverhalte messbar und klassifizierbar gemacht zu haben. Dazu verwendet man all jene Ausdrücke mit den Lösungen x1, x2, ..., deren Wert gleich 0 ist. Bei der vorliegenden Gleichung gehören dazu Ausrücke wie x1x3 + x2x4 oder auch
(x2 + x4 + x1 x2 x3 x4)2 + 4 x1 x2 x3 x4.
Die Gesamtheit der Ausdrücke mit Wert 0 ist als ganzes nur schwer überschaubar. Galois entwickelte aber eine elegante Methode, die für die Gleichungsauflösung wesentlichen Daten zu charakterisieren. Dies geschieht konkret dadurch, dass man alle möglichen Wege sucht, die Lösungen x1, x2, ... so miteinander zu vertauschen, dass jeder Ausdruck mit Wert 0 diesen nicht verändert.
Werden beispielsweise die Lösungen x1 und x2 einerseits und x3 und x4 andererseits miteinander vertauscht, dann wandelt sich der erste Ausdruck x1x3 + x2x4 zu x2x4 + x1x3, bleibt also unverändert. Der zweite Ausdruck
(x2 + x4 + x1 x2 x3 x4)2 + 4 x1 x2 x3 x4
verwandelt sich zu
(x1 + x3 + x2 x1 x4 x3)2 + 4 x1 x2 x3 x4,
allerdings bleibt der Wert 0 erhalten!
Unter den 4! ("4 Fakultät") = 4·3·2·1 = 24 möglichen Vertauschungen der vier Lösungen gibt es insgesamt acht Vertauschungen, die alle Ausdrücke mit Wert 0 wertmäßig unverändert lassen. Sie zusammen bilden die Galois-Gruppe. Dazu zählt natürlich auch jene "Vertauschung" p0, die alles auf seinem Platz beläßt. Die mit p4 bezeichnete Vertauschung ist die schon beschriebene:

Dass diese Vertauschungen den Wert 0 eines
Ausdrucks unverändert lassen, kann mit einem allgemeinen
Verfahren von Galois bestätigt werden (siehe Kasten). Umgekehrt
verliert durch jede andere Vertauschung mindestens ein Ausdruck
seinen Wert 0. Werden zum Beispiel nur die Lösungen x1
und x2 miteinander vertauscht, dann ändert sich der
Wert von x1x3 + x2x4
= 0 in ![]()
| Die
Bestimmung der Galois-Gruppe Die Suche nach allen aus den Lösungen x1, x2, ... gebildeten Ausdrücken mit Wert 0 ist in der Praxis kaum realisierbar (was die theoretische Bedeutung allerdings nicht schmälert). Zwar können immer endliche viele "Basis"-Ausdrücke gefunden werden, aus denen die (unendliche) Gesamtheit durch einfache Formeln abgeleitet werden kann. Wären solche Basis-Ausdrücke bekannt, müßten die Vertauschungen der Lösungen nur an ihnen getestet werden. Noch einfacher geht es aber mit einem Verfahren von Galois, bei dem sogar nur ein einziger Ausdruck getestet werden braucht. Man beginnt damit, einen Ausdruck zu suchen, der bei allen möglichen Vertauschungen lauter verschiedene Werte annimmt. Meist erfüllt bereits eine "Zufalls"-Wahl die gewünschte Eigenschaft, bei der Gleichung vierten Grades beispielsweise t = -x2 + x3 - 2x4. Galois bewies, dass es immer einen solchen, heute Galois-Resolvente genannten Ausdruck t gibt und dass er dann stets die folgende, wichtige Eigenschaft erfüllt: Alle Lösungen x1, x2, ... können allein mit Hilfe von Grundoperationen aus t und den Koeffizienten der Gleichung berechnet werden. Jedem Ausdruck der Lösungen x1, x2, ... entspricht daher ein Ausdruck in t, so dass alle Aussagen über Ausdrücke der Lösungen x1, x2, ... in Aussagen über Ausdrücke mit dem einzigen Wert t übersetzt werden können. Damit wird es möglich, die Wirkung der Vertauschungen ausschließlich anhand der Wirkung auf den Wert von t zu untersuchen. Und das geht am besten, wenn man eine möglichst einfache Gleichung konstruiert, die t als Lösung hat und deren Koeffizienten durch Grundoperationen aus denen der Ausgangsgleichung berechnet werden können. Beispielsweise erfüllt die oben angeführte Galois-Resolvente für die untersuchte Gleichung vierten Grades die Gleichung t8 + 16 t7 - 40 t6 - 1376 t5 - 928 t4 + 34048 t3 + 22208 t2- 253184 t + 72256 = 0. Interpretiert man diese, nicht mehr zu vereinfachende Gleichung in der Form (-x2 + x3 - 2x4) 8 + 16(-x2 + x3 - 2x4) 7 + ... = 0, so kann die Galois-Gruppe allein anhand daran gefunden werden: Für eine Vertauschung der zur ursprünglichen Gleichung gehörenden Lösungen x1, x2, ... muss nämlich geprüft werden, ob bei ihr die Gültigkeit der Gleichung bestehen bleibt oder nicht. Offensichtlich geht das nur, wenn mit der Vertauschung der Wert von t in eine andere Lösung der Gleichung achten Grades überführt wird. Diese acht Lösungen entsprechen damit genau den Vertauschungen der Galois-Gruppe: -x2 + x3 - 2x4, -x2 + x1 - 2x4, ..., -x3 + x2 - 2x1. |
Mit der Galois-Gruppe ist ein vorläufiger Endpunkt bei der Analyse einer Gleichung erreicht: Ohne Rückgriff auf die ursprüngliche Gleichung kann nämlich allein anhand der Galois-Gruppe entschieden werden, ob die Gleichung auflösbar ist oder nicht. Mehr noch: Bei auflösbaren Gleichungen gehen sogar die zur Auflösung notwendigen Wurzelgrade aus der Galois-Gruppe hervor.
Für solche Aussagen ist nicht nur die Größe der Galois-Gruppe von Bedeutung. Eine Rolle spielen im gewissen Rahmen auch die Vertauschungen selbst, wobei es allerdings einzig auf Beziehungen ankommt, wie sie zwischen den Vertauschungen der Galois-Gruppe bestehen. Eine Möglichkeit, diese vollständig zu tabellieren, ist die so genannte Gruppentafel (siehe Kasten). So kann dann allein anhand der Gruppentafel (oder einer äquivalenten Beschreibung der Gruppe) entschieden werden, ob eine Gleichung auflösbar ist oder nicht!
| Die
Gruppentafel einer Galois-Gruppe Führt man zwei Vertauschungen der Galois-Gruppe nacheinander aus, dann entsteht wieder eine Vertauschung. Lässt jede der beiden Vertauschungen bei Ausdrücken den Wert, sofern er gleich 0 ist, unverändert, dann gilt dies auch für die zusammengesetzte Vertauschung. Diese gehört damit ebenfalls zu Galois-Gruppe. Als Beispiel nehmen wir die Vertauschungen p1 und p6 der hier konstruierten Galois-Gruppe. Die Lösung x1 wird durch die Vertauschung p1 auf die Stelle von x3 geschoben. Da x3 von der zweiten Vertauschung p6 nach x4 geschoben wird, ergibt sich für x1 insgesamt ein Wechsel nach x4. Für die anderen Lösungen verfährt man entsprechend und erhält:
Ein Blick auf die Tabelle der Vertauschungen zeigt, dass es sich bei der zusammengesetzten Vertauschung um p7 handelt. Bei der Gruppentafel handelt es sich ähnlich wie bei einer Einmal-Eins-Tafel um eine Tabelle, in der alle Möglichkeiten, zwei Vertauschungen nacheinander auszuführen, zusammengestellt sind. Tabelliert sind also alle Ergebnisse der Form "erst p und dann q":
Alle Beziehungen, wie sie zwischen den Vertauschungen bestehen, können aus der Gruppentafel ersehen werden. Nicht mehr erkennbar ist, wie die Lösungen durch die Vertauschungen bewegt werden. |
Die Auflösung einer Gleichung
Wie kann eine so enge Beziehung zwischen der Auflösung einer Gleichung und ihrer Galois-Gruppe zustande kommen? Zumindest ansatzweise soll hier angedeutet werden, warum die Galois-Gruppe einer auflösbaren Gleichung ganz bestimmte Eigenschaften haben muss. Dazu ist zunächst der Prozess einer Gleichungsauflösung detailliert zu charakterisieren. Um Komplikationen zu vermeiden, etwa dass einige Lösungen durch Wurzelausdrücke dargestellt werden können und andere nicht, werden nur solche Gleichungen untersucht, die nicht sofort vereinfacht werden können. Das heißt, keine Lösung x1, ... xn darf eine Gleichung erfüllen, die einfacher ist als die ursprüngliche – also mit niedrigerem Grad und Koeffizienten, die mittels Grundoperationen aus denen der Ausgangsgleichung hervorgehen können. Ein Resultat der Galois-Theorie besagt, dass dies gleichbedeutend damit ist, dass jede Lösung auf eine beliebige andere Lösung mit zumindest einer Vertauschung aus der Galois-Gruppe geschoben werden kann.
Der Auflösungsprozess einer Gleichung verläuft, sofern er überhaupt möglich ist, immer schrittweise. Zur Abgrenzung der einzelnen Schritte bieten sich die Wurzeln als herausragende Operationen an. Dabei geht der Radikand jeweils unter ausschließlicher Verwendung der vier Grundoperationen aus Werten vorangegangener Schritte sowie aus Koeffizienten der Gleichung hervor. Es lässt sich zudem immer einrichten, dass alle Wurzelgrade Primzahlen sind.
Beispielsweise kann Gleichung die schon untersuchte Gleichung vierten Grades
x4 - 4x3 - 4x2 + 8x - 2 = 0
aufgelöst werden:
![]()
![]()
Die drei Auflösungsschritte werden durch die Zwischenwerte
![]()
markiert. Aus ihnen und den Koeffizienten ergeben sich schließlich alle vier Lösungen durch Grundoperationen.
Fortgesetzte Auslese von Vertauschungen
Die einzelnen Schritte der Gleichungsauflöung können nun in Beziehung zur Galois-Gruppe gesetzt werden. Dazu wird innerhalb der Galois-Gruppe ein schrittweiser Ausleseprozess konstruiert, dessen Schritte exakt den Schritten der Auflösung entsprechen. Dies geschieht dadurch, dass die zur Definition der Galois-Gruppe verwendete Gesamtheit von Ausdrücken mit den Lösungen x1, x2, ... mit jedem Auflösungschritt erweitert wird. Konkret wird jeweils jeder Ausdruck zugelassen, dessen Wert aus den Koeffizienten der Gleichung und allen vorangegangenen Zwischenwerten durch Grundoperationen hervorgehen kann. Wie bei der Konstruktion der Galois-Gruppe werden schließlich alle Vertauschungen herausgesucht, die bei der nun vergrößerten Gesamtheit von Ausdrücken die Werte unverändert lassen.
Durch die ansteigenden Anforderungen erhält man in jedem Schritt höchstens die Vertauschungen des vorangegangenen Schrittes, meist jedoch deutlich weniger. Insgesamt ergibt sich daher ein Ausleseprozess innerhalb der Galois-Gruppe.
Als Beispiel für den beschriebenen Ausleseprozess bieten sich die Zwischenwerte der für die Gleichung vierten Grades gegebenen Auflösung an:
Aufgrund des ersten Zwischenwertes ![]() vergrößert sich die
in Betracht zu ziehende Gesamtheit von Ausdrücken beispielsweise
um
vergrößert sich die
in Betracht zu ziehende Gesamtheit von Ausdrücken beispielsweise
um ![]() . Unter den
acht Vertauschungen der Galois-Gruppe fallen p4, p5,
p6 und p7 der Auslese zum Opfer, da sie auf
der linken Seite der Gleichung das Vorzeichen ändern. Hingegen
lassen die Vertauschungen p0 bis p3 den
fraglichen, aber auch die anderen dazugekommenen Ausdrücke
wertmäßig unverändert.
. Unter den
acht Vertauschungen der Galois-Gruppe fallen p4, p5,
p6 und p7 der Auslese zum Opfer, da sie auf
der linken Seite der Gleichung das Vorzeichen ändern. Hingegen
lassen die Vertauschungen p0 bis p3 den
fraglichen, aber auch die anderen dazugekommenen Ausdrücke
wertmäßig unverändert.
Kommt dann noch der zweite Zwischenwert ![]() hinzu, sind zusätzlich
Ausdrücke wie
hinzu, sind zusätzlich
Ausdrücke wie
![]()
und
![]()
bei der Auslese der Vertauschungen zu berücksichtigen.. Von den bislang verbliebenen Vertauschungen p0 bis p3 lassen nur p0 und p2 den Wert von x1 - x3 unverändert, während die beiden anderen ein Vorzeichenwechsel bewirken.
Der dritte Zwischenwert ist darstellbar durch
![]()
von den Vertauschungen p0 und p2 bleibt nur noch die erste übrig, da p2 bei x2 - x4 das Vorzeichen ändert. Dass – wie nach jeder vollständigen Gleichungsauflösung – keine echte Vertauschung mehr übrig geblieben sein kann, ist auch daran zu erkennen, dass alle Lösungen x1,..., x4 mittels Grundoperationen aus den Zwischenwerten bestimmt werden können.

Im Auflösungsprozess notwendige Grundoperationen sind nicht dargestellt.
Wie Wurzeln in der Galois-Gruppe wirken
Wie schon anhand des Beispiels zu vermuten ist, kann ein einzelner Ausleseschritt innerhalb der Galois-Gruppe keineswegs beliebige Formen annehmen, vielmehr gilt folgende Gesetzmäßigkeit: Bewirkt eine Wurzel mit Primzahlgrad p überhaupt eine echte Auslese, dann lassen sich die Vertauschungen vor dem Ausleseprozess in p gleich große Klassen einteilen, wobei eine Klasse genau die nach der Auslese übrigbleibenden Vertauschungen umfasst. Sortiert man außerdem die Vertauschungen am linken und oberen Rand der Gruppentafel klassenweise, dann zerfällt das Innere in p2 gleich große Teilquadrate, von denen jede nur Vertauschungen aus einer einzigen Klasse enthält.
Zur Erläuterung bietet sich wieder das Beispiel an (weitergehende Information grundsätzlicher Art findet man im Kasten): Für den ersten Schritt müssen die Vertauschungen nicht umsortiert werden, da sie bereits oben entsprechend den beiden Klassen, nämlich p0 bis p3 einerseits und p4 bis p7 andererseits, angelegt ist. Die Zerlegung der Gruppentafel in vier Teilquadrate, die jeweils nur die Vertauschungen einer Klasse enthalten, ist daher offensichtlich.
Das aus ihnen gebildete obere Teilquadrat kann nun so umsortiert werden, dass die Zerlegung zur Auslese nach p0, p2 möglich wird:
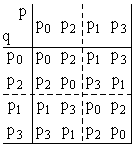
Der noch ausstehende Teil des Auflösungsprozesses wird durch das Teilquadrat oben links charakterisiert. Es kann sofort in vier 1×1-Teilquadrate zerlegt werden, was dem zweiten Auflösungsschritt entspricht.
Nicht alle Gleichungen sind auflösbar!
Wie dargelegt muss es für Galois-Gruppen von auflösbaren Gleichungen immer einen Ausleseprozess geben, der von der vollen Gruppe bis zur Vertauschung p0 verläuft und dessen Schritte die beschriebene Klasseneinteilung aufweisen. Daher folgt im Umkehrschluss, dass eine Gleichung, in deren Galois-Gruppe solches unmöglich ist, nicht auflösbar sein kann. Ein Beispiel ist die schon genannte Gleichung x5 - x - 1 = 0, deren Galois-Gruppe 120 Vertauschungen enthält. Möglich zunächst nur eine Zerlegung in vier Teilquadrate, allerdings kann das dabei entstehende 60×60-Teilquadrat selbst nicht mehr weiter zerlegt werden! Ist man bereit, auf jegliche mathematische Eleganz zu verzichten, kann sogar ein Computer solche Resultate bestätigen.
Nicht auflösbar sind, von seltenen Exoten wie etwa der Gleichung x5 + 15x - 44 = 0 (die Galois-Gruppe enthält 10 Vertauschungen) abgesehen, auch andere Gleichungen fünften Grades. Die Auflösbarkeit von Gleichungen fünften und höheren Grades wird somit zur Ausnahmeerscheinung.
Mit der Galois-Theorie lässt sich aber nicht nur die Nicht-Auflösbarkeit einer Gleichung nachweisen. Umgekehrt können zu jedem Ausleseprozess, der die beschriebenen Eigenschaften besitzt, Wurzelformeln für sämtliche Lösungen abgeleitet werden. Auflösung einer Gleichung und Ausleseprozess innerhalb der Galois-Gruppe sind damit vollkommen äquivalent! Diese enge Korrespondenz zwischen Gleichung und Auflösungsprozess einerseits und Galois-Gruppe und Ausleseprozess andererseits ist die Essenz von Galois Entdeckung. In der Fachsprache wird dem auch in der Bezeichnung Rechnung getragen: Was hier Ausleseprozess genannt wird, nennt man schlicht "Auflösung einer Gruppe".
| Wie
Vertauschungen bei Wurzelausdrücken wirken Im untersuchten Beispiel halbiert sich bei jedem Auflösungsschritt die Zahl der Vertauschungen. Am besten lässt das erkennen, wenn man die neu hinzugekommenen Zwischenwerte
jeweils durch einen Ausdruck der
Lösungen x1, x2, ... darstellt.
Dann kann nämlich der Ausleseschritt allein anhand von
diesem Ausdruck vorgenommen werden. Eine Hälfte der zu
prüfenden Vertauschungen lässt nämlich den Wert des
Ausdrucks unverändert, während die andere sein
Vorzeichen ändert. Es lässt sich zeigen, dass
entsprechendes immer der Fall ist, allerdings müssen bei
höheren Wurzelgraden auch nicht-reelle Wurzeln der 1
herangezogen werden. Beispielsweise beginnt die
Auflösung der schon angeführten Gleichung x2 - 3x2 - 3x - 1 = 0,
deren Galois-Gruppe drei Vertauschungen umfasst, mit dem
Zwischenwert
kann nun die Auslese vorgenommen werden. Die dritte Potenz ist gleich einer ganzen Zahl, also bleibt (x12 - 3 x1 - 2)3 bei Vertauschungen der Galois-Gruppe wertmäßig unverändert. Für den Ausdruck x12 - 3 x1 - 2 hat das zur Folge, dass die Vertauschungen der Galois-Gruppe eine Multiplikation mit einer dritten Wurzel von 1 bewirken. Beispielsweise ist
|
Literatur über Galois-Theorie
Galois Theory, Harold M. Edwards. Springer, New York 1984 (enthält u.a. die kommentierte Originalarbeit von Galois).
,Galoissche Theorie, E. Artin. Harri Deutsch, Zürich 1973.
Algebra, Band I., B.L.van der Waerden. Springer, Berlin 1971.
Das kurze Leben des Evariste Galois, Tony Rothman, Spektrum der Wissenschaft, Juni 1982.
| Mehr zu diesem Thema in meinem Buch "Algebra für Einsteiger: Von der Gleichungsauflösung zur Galois-Theorie", 242 + XXII Seiten, Vieweg-Verlag, 6. Auflage, Springer, Wiesbaden 2019, DOI: 10.1007/978-3-658-26152-8, (Vorwort). Das Buch behandelt, deutlich ausführlicher als die vorliegende Übersicht, die Auflösung von Gleichungen (u.a. Cardanische Formel, Kreisteilungsgleichungen), die Galois-Theorie sowie deren Anwendung auf geometrische Konstruktionsaufgaben (Quadratur des Kreises, Winkeldreiteilung, Kubusverdoppelung, regelmäßiges Siebzehneck). |