Galois theory is the culmination of a centuries-long search for a solution to the classical problem of solving algebraic equations by radicals. In this book, Bewersdorff follows the historical development of the theory, emphasizing concrete examples along the way. As a result, many mathematical abstractions are now seen as the natural consequence of particular investigations.
Few prerequisites are needed beyond general college mathematics, since the necessary ideas and properties of groups and fields are provided as needed. Results in Galois theory are formulated first in a concrete, elementary way, then in the modern form. Each chapter begins with a simple question that gives the reader an idea of the nature and difficulty of what lies ahead. The applications of the theory to geometric constructions, including the ancient problems of squaring the circle, duplicating the cube, and trisecting an angle, and the construction of regular n-gons are also presented.
This book is suitable for undergraduates and beginning graduate students.
Readership
Undergraduates and graduate students interested in Galois Theory.
Preface to the English Edition vii
Prefaces to the German Editions ix
Chapter 1. Cubic Equations 1
Chapter 2. Casus Irreducibilis: The Birth of the Complex
Numbers 9
Chapter 3. Biquadratic Equations 23
Chapter 4. Equations of Degreen and Their Properties 27
The Fundamental Theorem of Algebra: Plausibility and Proof 32
Chapter 5. The Search for Additional Solution Formulas 37
Permutations 42
The Fundamental Theorem on Symmetric Polynomials 47
Ruffini and the General Equation of Fifth Degree 50
Chapter 6. Equations That Can Be Reduced in Degree 55
The Decomposition of Integer Polynomials 57
Eisenstein’s Irreducibility Criterion 60
Chapter 7. The Construction of Regular Polygons 63
Constructions with Straightedge and Compass 69
The Classical Construction Problems 74
Chapter 8. The Solution of Equations of the Fifth Degree 81
The Transformations of Tschirnhaus and of Bring and
Jerrard 89
Chapter 9. The Galois Group of an Equation 93
Computing the Galois Group 114
A Quick Course in Calculating with Polynomials 119
Chapter 10. Algebraic Structures and Galois Theory 125
Groups and Fields 130
The Fundamental Theorem of Galois Theory: An
Example 144
Artin’s Version of the Fundamental Theorem of
Galois Theory 149
The Unsolvability of the Classical Construction
Problems 161
Epilogue 165
Index 177
But back to Cardano. In addition to the solution for cubic equations,
Cardano published in his Ars Magna a general formula for
quartic equations, that is, equations of the fourth degree, also known
as biquadratic equations.
With the almost simultaneous discovery of formulas for solving
third- and fourth-degree equations came the inevitable problem of
finding similar formulas for equations of higher degree (e.g. for quintics). To accomplish
this, the techniques that were used for the cubic and quartic equations
were systematized, already in Cardano’s time, so that they could be
applied to equations of the fifth degree. But after three hundred years
of failure, mathematicians began to suspect that perhaps there were
no such formulas after all.
This question was resolved in 1826 by Niels Henrik Abel (1802–
1829), who showed that there cannot exist general solution formulas
for equations of the fifth and higher degree that involve only the usual
arithmetic operations and extraction of roots. One says that such
equations cannot besolved in radicals. The heart of Abel’s proof is
that for the intermediate values that would appear in a hypothetically
existing formula, one could prove corresponding symmetries among
the various solutions of the equation that would lead to a contradiction.
Galois Theory
A generalization of Abel’s approach, which was applicable
to all polynomial equations, was found a few years later by
the twenty-year-old Evariste Galois (1811–1832). He wrote down the
results of his researches of the previous few months on the evening
before he was killed in a duel.
Of much greater significance than such solutions is the method
that Galois discovered, which was unorthodox, indeed revolutionary,
at the time, but today is quite usual in mathematics. What Galois
did was to establish a relationship between two completely different
types of mathematical objects and their properties. In this way he
was able to read off the properties of one of these objects, namely
the solvability of a given equation and the steps in its solution, from
those of the corresponding object.
But it was not only the principle of this approach that benefited
future mathematics. In addition, the class of mathematical objects
that Galois created for the indirect investigation of polynomial equations
became an important mathematical object in its own right, one
with many important applications. This class, together with similar
objects, today forms the foundation of modern algebra, and other
subdisciplines of mathematics have also progressed along analogous
paths.
The object created by Galois that corresponds to a given equation,
called today the Galois group, can be defined on the basis of
relations between the solutions of the equation in the form of identities
such as x12= x2 + 2. Concretely, the Galois group consists of
renumberings of the solutions. Such a renumbering belongs to the
Galois group precisely if every relationship is transformed by this
renumbering into an already existing relationship. Thus for the case
of the relation x12= x2 + 2 in our example, the renumbering corresponding
to exchanging the two solutions x1 and x2 belongs to the
Galois group only if the identity x22= x1 + 2 is satisfied. Finally,
every renumbering belonging to the Galois group corresponds to a
symmetry among the solutions of the equation. Moreover, the Galois
group can be determined without knowledge of the solutions.
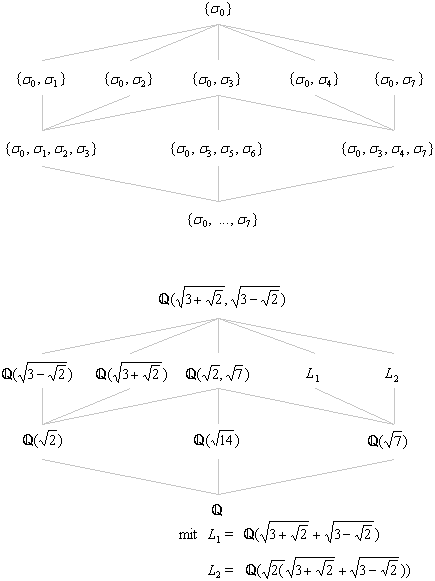
The Galois group can be described by a finite table that is elementary
but not particularly elegant. Such a table is called a group
table, and it can be looked upon as a sort of multiplication table, in
which each entry is the result of operating on two elements of the Galois
group in succession. An example is shown in Figure 0.1. What is
significant about the Galois group, and its corresponding group table,
is that it always contains the information about whether, and if so,
how, the underlying equation can be solved in radicals. To be sure,
the proof of this in a concrete application can be quite involved; nevertheless,
it can always be accomplished in a finite number of steps
according to a fixed algorithm.
Today, Galois’s ideas are described in textbooks in a very abstract
setting. Using the class of algebraic objects that we previously
mentioned, it became possible at the beginning of the twentieth century
to reformulate what has come to be called Galois theory, and
indeed in such a way that the problem itself can be posed in terms
of such objects. More precisely, the properties of equations and their
solution can be characterized in terms of associated sets of numbers
whose common characteristic is that they are closed under the four
basic arithmetic operations. These sets of numbers are called fields.