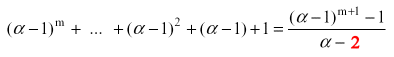---

Einführung
zum Buch von Jörg Bewersdorff:
Glück, Logik und Bluff:
Mathematik im Spiel - Methoden, Ergebnisse und Grenzen

Das Abenteuergefühl ist ein Element des Spiels. Wir setzen uns der Ungewißheit des Schicksals aus und erleben, wie wir es durch unsere eigene Tätigkeit in den Griff bekommen.

Alex Randolph, Spieleautor

Die Ungewißheit im Gesellschaftsspiel

Warum spielen wir? Woher rührt der Reiz eines Spiels? Was bringt Menschen dazu, oft stundenlang zu spielen? Wo bleibt die Langweile, wenn immer wieder das gleiche Spiel gespielt wird? Wirklich das gleiche Spiel?

Wirklich gleich bleiben bei einem Spiel nur seine Regeln, Verlauf und Ausgang ändern sich hingegen von Partie zu Partie. Die Zukunft bleibt zunächst im Dunklen – wie im richtigen Leben, aber auch wie im Roman, im Spielfilm und beim sportlichen Spiel. Das sorgt für Unterhaltung und erzeugt zugleich Spannung.

Verstärkt wird die Spannung durch die Möglichkeit zum Gewinn. Jeder Spieler hofft zu gewinnen – um einen materiellen Gewinn zu erlangen, in der Hoffnung auf ein kurzes Glücksgefühl, als Selbstbestätigung oder im Hinblick auf Anerkennung. Egal, um was es "geht", jeder Spieler kann hoffen. Sogar ein Verlierer darf wieder Hoffnung schöpfen, wenn das Spiel weiter geht: "Neues Spiel – neues Glück". Dabei wirkt die Hoffnung auf einen Gewinn oft stärker als das Wissen über schlechte Gewinnchancen. Die Popularität von Kasino- und Lotteriespielen beweist das ständig neu.

Unterhaltung und allseitige Gewinnhoffnung haben dieselbe Basis, nämlich die Abwechslung im Spiel. Durch sie bleiben die Spieler lange im Ungewissen über die weitere Entwicklung einer Partie bis hin zu deren Resultat. Wie aber kommt es zu dieser Ungewißheit? Welche Mechanismen des Spiels verursachen sie? Bereits anhand von Spielen wie Roulette, Schach und Pokern lassen sich drei prinzipiell verschiedene Typen von Ursachen erkennen:

1. Zufall.
2. Vielfältige Kombinationen der möglichen Züge.
3. Unterschiedlicher Informationsstand der einzelnen Spieler.

1. Zufällige Einflüsse treten bei Gesellschaftsspielen in der Hauptsache beim Würfeln auf, ebenso beim Mischen von Spielkarten und -steinen. Der Verlauf einer Partie wird dann im Rahmen der Spielregeln sowohl von Entscheidungen der Spieler, als auch den Ergebnissen zufälliger Prozesse bestimmt. Dominiert der Einfluß des Zufalls gegenüber denen der Spieler, spricht man von Glücksspielen. Bei reinen Glücksspielen ist die Entscheidung eines Spielers über die Teilnahme und die Höhe des Einsatzes bereits die wichtigste. Glücksspiele, die um Geld gespielt werden, unterliegen traditionell gesetzlichen Reglementierungen^, .

2. Im allgemeinen erhalten die Spieler während des Verlaufs einer Partie in genau festgelegten Situationen die Gelegenheit zu handeln. Zur Auswahl stehen dabei bestimmte, durch die Spielregeln fixierte Handlungsmöglichkeiten. Ein Spielabschnitt, der genau eine solche Handlungsmöglichkeit eines Spielers umfaßt, wird Zug genannt. Bereits nach wenigen Zügen können sich die erlaubten Möglichkeiten zu einer kaum noch überschaubaren Vielfalt kombinieren, so daß die Konsequenzen eines einzelnen Zuges nur noch schwer zu erkennen sind. Genau diesem Umstand verdanken Schachaufgaben vom Typ "Matt in zwei Zügen" ihre Schwierigkeit. Spiele, bei denen die Ungewißheit ganz auf den vielfältigen Zugmöglichkeiten beruht, werden kombinatorische Spiele genannt. Bekannte Vertreter dieser Klasse von Spielen sind Brettspiele wie Schach, Go, Mühle, Dame, Halma und Reversi. Zu den Spielen, die sowohl kombinatorische wie zufällige Elemente besitzen, gehören Backgammon und "Mensch ärgere dich nicht", wobei der kombinatorische Charakter beim Backgammon deutlich ausgeprägter ist als beim "Mensch ärgere dich nicht".

3. Eine dritte Ursache, die bei Spielern eine Ungewißheit über den weiteren Spielverlauf verursachen kann, entsteht, wenn die Spieler unterschiedliche Informationen über den erreichten Spielstand besitzen und damit ein einzelner Spieler nicht unbedingt die Informationen hat, über die die Spieler insgesamt verfügen. So muß ein Pokerspieler seine Entscheidungen treffen, ohne daß er die Karten seiner Gegner kennt. Man könnte nun argumentieren, daß auch beim Backgammon gezogen werden muß, ohne die künftigen Würfelergebnisse zu kennen. Jedoch besteht zwischen Pokern und Backgammon ein gravierender Unterschied: Die weiteren Würfelergebnisse kennt kein Spieler, hingegen sind die bereits verteilten Karten einem Teil der Spieler bekannt – jeder sieht zunächst nur seine eigenen Karten. Spiele, deren Teilnehmer vorwiegend aufgrund solcher imperfekter Information im Ungewissen über den weiteren Spielablauf sind, werden strategische Spiele genannt; in reiner Form sind sie allerdings sehr selten. Imperfekte Information ist ein typisches Element der meisten Kartenspiele wie Pokern, Skat und Bridge. Bei den Brettspielen Geister und Stratego beruht die imperfekte Information darauf, daß man zunächst nur den Ort, nicht aber den Typ der gegnerischen Steine kennt. Bei Diplomacy und Papier-Stein-Schere ziehen die Spieler gleichzeitig, so daß jedem Spieler die Information über den aktuellen Zug der Gegner fehlt. Wie sich die imperfekte Information in einem Spiel konkret auswirkt, läßt sich am besten verdeutlichen, wenn die Spielregeln so abgeändert werden, daß ein neues Spiel mit perfekter Information entsteht. Bei Kartenspielen müssen dazu die Spieler ihre Karten offen auslegen; Poker würde auf diese Weise zur Farce, Skat bliebe immerhin ein kombinatorisch interessantes Spiel ähnlich der halb-offenen Zwei-Personen-Variante. Neben dem Spiel Papier-Stein-Schere, bei dem es sich um ein rein strategisches Spiel handelt, erkennt man auf diese Weise auch Pokern als ein überwiegend strategisches Spiel.

Bild 1 Die drei Ursachen der Ungewißheit in Gesellschaftsspielen: Gewonnen wird mit Glück, Logik und Bluff.

Zu fragen bleibt, ob die Ungewißheit über den weiteren Spielverlauf noch auf anderen, bisher nicht erkannten Ursache beruhen kann. Untersucht man eine Vielzahl von Spielen nach solchen Ursachen, dann stößt man im wesentlichen auf die folgenden Erscheinungen:

• Das Ergebnis eines Spieles kann von der körperlichen Geschicklichkeit und Leistungsfähigkeit abhängen. Außer den Sport- und Computerspielen, die sicherlich nicht zu den Gesellschaftsspielen gehören, ist beispielsweise Mikado ein Spiel, das manuelle Geschicklichkeit erfordert.
• Die Spielregeln an sich können den Spielern zum Teil unklar sein. Insbesondere in der Lernphase komplizierter Spiele kommt es zu solchen Situationen. In anderen Fällen ergeben sich Zweifelsfälle zwangsläufig aus der Natur des Spiels. So kann es beim Kreuzworträtsel-artigen Spiel Scrabble unklar sein, ob ein Wort zulässig ist oder nicht. Und selbst beim Skat bleibt das in Altenburg tagende Skatgericht bei der Klärung von Streitfragen nicht unbeschäftigt, auch wenn es meist nur mit nebensächlichen Details befaßt ist.
• Ein unvollkommenes Gedächtnis vergrößert nicht beim nur Memory die persönliche Ungewißheit. Allerdings ist diese Art der Ungewißheit keine objektive Eigenschaft des betreffenden Spiels.

Im Vergleich zu Zufall, Kombinationsreichtum und unterschiedlichen Informationsständen können die zuletzt genannten Phänomene allesamt vernachläßigt werden. Keins von ihnen ist als typische und objektive Ursache für die Ungewißheit in einem Gesellschaftsspielen anzusehen.

Spiel und Mathematik

Will ein Spieler die Gewinnaussichten zu seinen Gunsten verbessern, muß er zunächst versuchen, seine persönliche Ungewißheit möglichst weitgehend zu überwinden, um dann die Konsequenzen seiner möglichen Handlungen abzuwägen. Wie er dabei vorzugehen hat, hängt selbstverständlich davon ab, welche konkreten Ursachen für seine Ungewißheit verantwortlich sind: Will ein Spieler beispielsweise entscheiden, ob er an einem Glücksspiel teilnehmen soll oder nicht, dann muß der die Gewinnchancen dahingehend abschätzen, ob sie im Vergleich zum Einsatz attraktiv sind. Ein Schachspieler dagegen hat zu seinem ins Auge gefaßten Zug alle möglichen Gegenzüge zu prüfen und zu jedem von ihnen mindestens eine erfolgreiche Antwort parat zu haben. Ein Pokerspieler schließlich muß versuchen zu ergründen, ob das hohe Gebot seines Gegners auf einem guten Blatt basiert oder ob es sich nur um einen Bluff handelt. Alle drei Probleme lassen sich nicht nur im Einzelfall spielerisch, sondern auch in prinzipieller Hinsicht untersuchen. Welche mathematische Methoden dafür entwickelt wurden, soll im vorliegenden Buch anhand von möglichst plakativen Beispielen vorgestellt werden:

• Glücksspiele können mit Hilfe der Wahrscheinlichkeitsrechnung analysiert werden. Diese mathematische Disziplin, die heute in vielfältiger Weise in Natur-, Wirtschafts- und Sozialwissenschaften angewendet wird, verdankt sogar ihre Entstehung im 17. Jahrhundert dem Wunsch, die Gewinnchancen von Glücksspielen berechnen zu können.
• Für die kombinatorischen Elemente in Spielen gibt es keine einheitliche Theorie. Jedoch können mit den unterschiedlichsten mathematischen Methoden sowohl prinzipielle als auch für Einzelfälle konkrete Resultate erzielt werden.
• Ausgehend von den strategischen Komponenten eines Spieles wurde eine eigene mathematische Disziplin begründet, die sogenannte Spieltheorie. Spiele fungieren dort als Modell, auf deren Basis interaktive, ökonomische Prozesse in Abhängigkeit von getroffenen Entscheidungen untersucht werden.

Für alle drei Spieltypen und ihre mathematischen Methoden gilt, daß mit Hilfe von Computern ansonsten unerreichbare Anwendungen realisiert werden können. Aber auch unabhängig von der Entwicklung immer schnellerer Computer hat es bei den betreffenden mathematischen Theorien im 20. Jahrhundert große Fortschritte gegeben. Das mag den einen oder anderen mathematischen Laien vielleicht überraschen – besitzt die Mathematik doch oft völlig zu unrecht den Ruf, ihre Entwicklung sei schon lange abgeschlossen.

Der Ausgangspunkt der Wahrscheinlichkeitsrechnung liegt in Fragen wie derjenigen, welcher Spieler in einem Glücksspiel die besten Chancen hat zu gewinnen. Zentraler Begriff ist die Wahrscheinlichkeit, die als Maß für die Gewißheit interpretiert werden kann, mit der ein zufälliges Ereignis eintritt. Für Glücksspiele interessiert natürlich letztlich die Wahrscheinlichkeit des Ereignisses, daß ein bestimmter Spieler gewinnt. Häufig muß aber nicht nur der Gewinn als solches, sondern zugleich auch seine Höhe berücksichtigt werden. Zu berechnen sind dann der durchschnittliche Gewinn und das mit dem Spiel verbundene Risiko. Aber nicht immer muß ein Spiel vollständig analysiert werden, beispielsweise dann, wenn nur unterschiedliche Zugmöglichkeiten gegeneinander abzuwägen sind und das im direkten Vergleich geschehen kann. Bei Wettrennen auf Würfelbasis stellen sich dabei Fragen der Art, wie lange ein Spielstein durchschnittlich dafür braucht, eine bestimmte Wegstrecke zurückzulegen. Besonders kompliziert sind solche Berechnungen dann, wenn wie beim Leiterspiel ein Spielstein auch wieder zurückfallen kann. Auch die Antwort auf die Frage nach der Bevorzugung von bestimmten Feldern beim Monopoly verlangt ähnliche Berechnungs-Techniken. Schwierig zu analysieren sind ebenso solche Glücksspiele, die ausgeprägte kombinatorische Spielelemente beinhalten. Erstmals bewältigt wurden solche Schwierigkeiten bei der Analyse des Black Jacks.

Kombinatorische Spiele, namentlich die traditionsreichen Vertreter Schach und Go, gelten als Spiele mit hohem intellektuellen Anspruch. Schon früh in der Entwicklungsgeschichte der Rechenmaschinen reifte daher der Wunsch heran, in Maschinen ebenbürtige Spielgegner finden zu können. Wie aber läßt sich das realisieren? Dafür benötigt werden Rechenverfahren, mit denen ausreichend gute Züge gefunden werden können. Kann die Güte eines Zuges aber überhaupt eindeutig bewertet werden oder hängt sie nicht immer von der gegnerischen Antwort ab? Immerhin ist der Suchverfahren und Computertechnik umfassende aktuelle Stand der Technik beeindruckend. Ein durchschnittlicher Schachspieler besitzt nämlich gegen die besseren Schachprogramme kaum noch eine Chance. Aber nicht nur Schach war Gegenstand des mathematischen Interesses. Für viele Spiele konnten, zum Teil auf überraschend einfache Weise, sichere Gewinnstrategien gefunden werden. Bei anderen Spielen kann seltsamerweise nur bestimmt, werden, welcher Spieler theoretisch stets gewinnen kann, ohne daß bis heute eine Gewinnstrategie konkret bekannt ist. Einige dieser Spiele besitzen sogar Eigenschaften, die kaum eine Hoffnung bestehen lassen, je eine solche Gewinnstrategie zu finden.

In welcher Weise sich strategische Spiele prinzipiell von zufälligen und kombinatorischen Spielen unterscheiden, davon handeln die Grundlagen der Spieltheorie. Am Beginn steht eine mathematisch formale Definition eines Spiels. Charakterisiert wird ein Spiel durch seine Regeln und diese umfassen die folgenden Angaben:

• Die Anzahl der Mitspieler.
• Zu jedem Spielstand die Aussage darüber,
  • wer am Zug ist,
  • welche Zugmöglichkeiten für den betreffenden Spieler bestehen und
  • auf Basis welcher Informationen er seine Entscheidung zu treffen hat.
• Für beendete Partien, wer wieviel gewonnen hat.
• Bei Zufallszügen, wie wahrscheinlich die möglichen Ergebnisse sind.

Als eigenständige Disziplin entstand die Spieltheorie erst 1944, als fast aus dem Nichts eine monumentale Monographie über die Theorie der Spiele erschien. Auch wenn sich dieses Werk an verschiedenen Stellen Spielen wie Schach, Bridge und Pokern widmet, sind für die Spieltheorie wirkliche Gesellschaftsspiele im Vergleich zu ökonomischen Prozessen eigentlich nachrangig. Daß sich Spiele überhaupt als Modell für reale Abläufe eignen, überrascht eigentlich nicht. Schließlich sind viele Spielelemente Konflikten um Geld, Macht oder gar Leben entlehnt. Insofern bietet es sich die "Umkehrung" geradezu an, daß heißt, die Interaktion von Individuen – ob in Konkurrenz oder in Kooperation – auf der Basis eines an Spielen angelehnten Modells zu beschreiben und untersuchen. Die weitgehende Idealisierung ist dabei genauso unvermeidbar, wie es bei anderen Modellen der Fall ist, etwa wenn in der Physik eine Masse als auf einen Punkt konzentriert angenommen wird.

Über dieses Buch

Entsprechend der beschriebenen Systematik gliedert sich der nachfolgende Text in drei Teile, in denen nacheinander zufällige, kombinatorische und strategische Spielelemente mathematisch untersucht werden. Jeder der drei Teile umfaßt mehrere Kapitel, die jeweils ein abgegrenztes Problem – meist ein einzelnes Spiel oder Spielelement – zum Gegenstand haben. Aufgrund der problemorientierten Auswahl differiert das mathematische Niveau bei den verschiedenen Kapiteln erheblich. Obwohl Bezüge auf vorangegangene Kapitel zahlreich sind, können die Kapitel oft unabhängig voneinander gelesen werden. Jedes Kapitel beginnt mit einer, manchmal mehr oder weniger rhetorisch gemeinten Frage, die zugleich Natur und Schwierigkeit des im betreffenden Kapitel behandelten Problems offenbart. Dem (der) mathematisch bestens vorgebildeten Leser(in), für den (die) der hier gebotene Überblick in vielen Fällen zu oberflächlich und unvollständig bleiben muß, ermöglicht diese Struktur eine schnelle und gezielte Auswahl der für ihn (sie) interessanten Teile – die angegebene Fachliteratur weist den weiteren Weg. Ebenso zum Weiterlesen anregen sollen die angeführten Zitate sowie die Ausblicke auf mathematische Hintergründe und verwandte, außerhalb des eigentlichen Themenbereichs liegende Probleme und Sachverhalte.

Deutlichen Wert gelegt wird auf die historische Entwicklung und zwar zum einen, weil zumindest der jüngere Aufschwung der Mathematik weit weniger bekannt ist als der der Naturwissenschaften, zum anderen, weil es durchaus spannend sein kann, persönlichen Irrtum und Erkenntnisgewinn der zeitraffermäßig verkürzten Entwicklung zuordnen zu können. Wie stark die mathematische Forschung auch im – nicht unbedingt repräsentativen – Bereich der Spiele gerade in den letzten Jahrzehnten vorangeschritten ist, macht ein Vergleich mit thematisch ähnlich abgegrenzten, im Detail allerdings oft anders ausgerichteten Zusammenstellungen deutlich, deren Erscheinen vor der Entdeckung vieler der hier beschriebenen Ergebnisse datiert ist:

• R. Vogelsang, Die mathematische Theorie der Spiele, Bonn 1963;
• N. N. Worobjow, Die Entwicklung der Spieltheorie, Berlin (-Ost) 1975 (russ. Orig. 1973) – Hauptgegenstand ist die Spieltheorie als mathematische Disziplin, jedoch wird für die Theorien von Glücksspielen, kombinatorischen und strategischen Spielen in I. §§2-5 ein Abriß der historischen Entwicklung gegeben;
• Richard A. Epstein, The theory of gambling and statistical logic, New York 1967 (erweiterte Neuauflage 1977);
• Edward Packel, The mathematics of games and gambling, Washington 1981.
• John D. Basley, The mathematics of games, Oxford 1989.
• La mathématique des jeux, Bibliothèque pour La Science, Paris 1997 - Beiträge zum Thema Spiel und Mathematik der französischen Ausgabe von Scientific American, die nur zum Teil auch in anderen Länderausgaben veröffentlicht wurden.

Nicht versäumen möchte ich es, meinen Dank an all jene auszusprechen, die bei der Entstehung dieses Buchs behilflich waren: Elwyn Berlekamp, Richard Bishop, Olof Hanner, Julian Henny, Daphne Koller, Martin Müller, Bernhard von Stengel und Baris Tan erläuterten mir freundlicherweise ihre Forschungsergebnisse. Bernhard von Stengel verdanke ich darüber hinaus einige Anmerkungen und Verbesserungsvorschläge und nicht zuletzt die Ermutigung, den Weg zu einer Publikation zu suchen. Angesichts des umfangreichen Quellenstudiums nicht vergessen werden soll die mir zuteil gewordene Unterstützung durch Mitarbeiter der von mir genutzten Bibliotheken – stellvertretend auch für die anderen seien hier nur die Bibliothek des Mathematischen Instituts in Bonn, die Bibliothek des Instituts für Diskrete Mathematik in Bonn sowie die Universitätsbibliotheken Bonn und Bielefeld genannt. Frauke Schindler vom Lektorat des Vieweg-Verlages und Karin Buckler haben viel dazu beigetragen, die Zahl meiner Fehler zu verringern. Dem Vieweg-Verlag, namentlich seiner Programmleiterin Ulrike Schmickler-Hirzebruch, habe ich dafür zu danken, diese sicher aus dem üblichen Rahmen fallende Zusammenstellung ins Verlagsprogramm aufgenommen zu haben. Last not least gilt mein ganz besonderer Dank meiner Frau Claudia, deren Verständnis ich in den letzten Jahren leider viel zu oft strapaziert habe.

Vorwort zur zweiten Auflage

Der erfreuliche Umstand, dass die erste Auflage nach nur zwei Jahren vergriffen ist, gibt mir Gelegenheit, zwischenzeitlich entdeckte Druckfehler zu beseitigen. Außerdem konnten einige Literaturverweise und Hinweise auf neuere Untersuchungen ergänzt werden. Danken möchte ich Hans Riedwyl, Jürg Nievergelt und Avierzi S. Fraenkel für ihre Anmerkungen.

Hinweisen möchte ich schließlich noch auf meine Web-Seite www.bewersdorff-online.de, auf der ich Ergänzungen und Korrekturen veröffentliche.

 

Jörg Bewersdorff

---

Inhaltsverzeichnis

Einführung

Die Ungewißheit im Gesellschaftsspiel

Spiel und Mathematik

Über dieses Buch

---

1. Glücksspiele

1.1 Würfel und Wahrscheinlichkeit

1.2 Warten auf die Doppel-Sechs

1.3 Lottotips – "gleicher als gleich"?

1.4 Gerecht teilen – aber wie?

1.5 Rot und Schwarz – das Gesetz der großen Zahlen

1.6 Unsymmetrische Würfel: Brauchbar oder nicht?

1.7 Wahrscheinlichkeit und Geometrie

1.8 Zufall und mathematische Bestimmtheit – unvereinbar?

1.9 Die Suche nach dem Gleichmöglichen

1.10 Gewinne im Spiel: Wahrscheinlichkeit und Wert

1.11 Welcher Würfel ist der beste?

1.12 Ein Würfel wird getestet

1.13 Die Normalverteilung: Wie lange braucht man ins Ziel?

1.14 Nicht nur beim Roulette: Die Poisson-Verteilung

1.15 Wenn Formeln zu kompliziert sind: Die Monte-Carlo-Methode

1.16 Markow-Ketten und Monopoly

1.17 Black Jack: Ein Märchen aus Las Vegas

---

2. Kombinatorische Spiele

2.1 Welcher Zug ist der beste?

2.2 Gewinnaussichten und Symmetrie

2.3 Ein Spiel zu dritt

2.4 Nim: Gewinnen kann ganz einfach sein!

2.5 Lasker-Nim: Gewinn auf verborgenem Weg

2.6 Schwarz-Weiß-Nim: Jeder zieht mit seinen Steinen

2.7 Ein Spiel mit Domino-Steinen: Wie lange ist noch Platz?

2.8 Go: Klassisches Spiel mit moderner Theorie

2.9 Misère-Spiele: Verlieren will gelernt sein!

2.10 Der Computer als Spielpartner

2.11 Gewinnaussichten – immer berechenbar?

2.12 Spiele und Komplexität: Wenn Berechnungen zu lange dauern

2.13 Memory: Gutes Gedächtnis und Glück – sonst nichts?

2.14 Backgammon: Doppeln oder nicht?

2.15 Mastermind: Auf Nummer sicher

---

3. Strategische Spiele

3.1 Papier-Stein-Schere: Die unbekannten Pläne des Gegners

3.2 Minimax kontra Psychologie: Selbst beim Pokern?

3.3 Poker-Bluff: Auch ohne Psychologie?

3.4 Symmetrische Spiele: Nachteile sind vermeidbar, aber wie?

3.5 Minimax und Lineare Optimierung: So einfach wie möglich

3.6 Play it again: Aus Erfahrung klug?

3.7 Le Her: Tauschen oder nicht?

3.8 Zufällig entscheiden – aber wie?

3.9 Optimal handeln – effizient geplant

3.10 Baccarat: Ziehen bei Fünf?

3.11 Pokern zu dritt: Vertrauenssache?

3.12 "QUAAK!" – (k)ein Kinderspiel

3.13 Mastermind: Farbcodes und Minimax

Stichwortverzeichnis

Anmerkungen

Und leider notwendig: Korrekturen

---

1. Glücksspiele
   1. Würfel und Wahrscheinlichkeit
      Mit einem Würfelpaar kann die Summe 10 durch 5+5 oder 6+4 erreicht werden. Auch die Summe 5 läßt sich auf zwei Arten, nämlich durch 1+4 oder 2+3, erzielen. Trotzdem tritt die Würfelsumme 5 in längeren Versuchsreihen erfahrungsgemäß häufiger als die 10 auf. Warum?
      Begriffe: Ereignis, Wahrscheinlichkeit, gleichmögliche Fälle, Laplace-Modell, Gesetz der großen Zahlen
      
   2. Warten auf die Doppel-Sechs
      Wettet man darauf, in vier Würfen mit einem Würfel mindestens eine Sechs zu erzielen, dann ist erfahrungsgemäß ein Gewinn eher wahrscheinlich als ein Verlust. Wie sieht es aber mit der Variante aus, bei der mit zwei Würfeln mindestens eine Doppel-Sechs erzielt werden muß? Wie viele Versuche müssen eingeräumt werden, damit auch diese Wette empfehlenswert wird? Folgende Überlegung bietet sich an: Da eine Doppel-Sechs als eine von 36 gleichmöglichen Kombinationen nur ein Sechstel so wahrscheinlich ist wie eine Sechs mit einem Würfel, reichen sechsmal so viele Versuche. Somit scheint die Wette, in 24 Versuchen mindestens eine Doppel-Sechs zu erzielen, erfolgversprechend. Sollte man aber tatsächlich so wetten?
      Begriffe: Multiplikationsgesetz
      
   3. Lottotips – "gleicher als gleich"?
      Eine statistische Auswertung der insgesamt 1433 deutschen Lotto-Ausspielungen, die vom Oktober 1955 bis Anfang 1983 erfolgten, ergibt, daß – ohne Berücksichtigung der Zusatzzahlen – bei 76,4% der Ausspielungen mindestens eine der Zahlen von 1 bis 10 gezogen wurde. Getippte Zahlenreihen, die keine der Zahlen 1 bis 10 enthielten, hatten also allein aufgrund dieser Tatsache in 76,4% der Fälle keine Chance, einen Haupttreffer mit "Sechs Richtigen" zu erzielen. Sollte man deshalb immer mindestens eine der Zahlen 1 bis 10 in seinem Lotto-Tip berücksichtigen?
      Begriffe: Kombinatorik, Permutation, Fakultät, Binomialkoeffizient
      
   4. Gerecht teilen – aber wie?
      Zwei Spieler tragen ein Glücksspiel aus, das sich über mehrere Runden erstreckt, in denen die Gewinnchancen jeweils 50:50 sind. Den gesamten Einsatz soll der Spieler gewinnen, der als erster vier Runden für sich entscheidet. Als der Spielstand 3:2 erreicht ist, muß das Match vorzeitig abgebrochen werden. Man einigt sich darauf, die Einsätze dem Spielstand entsprechend fair zu teilen. Aber welches Teilungsverhältnis ist fair?
      Begriffe: Binomialverteilung
      
   5. Rot und Schwarz – das Gesetz der großen Zahlen
      Werden im Spielkasino beim Roulette zehn rote Zahlen hintereinander ausgespielt, setzt das Publikum erfahrungsgemäß kaum noch auf Rot. Der Grund ist naheliegend: Nach dem Übergewicht roter Zahlen erwartet man einen "Ausgleich", denn schließlich gibt es ja ein Gesetz der großen Zahlen, gemäß dem sich das Verhältnis zwischen Rot und Schwarz auf Dauer ausgleicht. Andererseits sind Roulette-Läufe voneinander unabhängig, denn die Kugel verfügt ebenso wenig über ein "Gedächtnis" wie ein Würfel. Folglich sind beide Farben auch nach zehnmal Rot noch völlig gleichwahrscheinlich. Wo liegt der Widerspruch?
      Begriffe: starkes Gesetz der großen Zahlen
      
   6. Unsymmetrische Würfel: Brauchbar oder nicht?
      Kann ein Würfel, der in Form oder Material unregelmäßig ist, trotzdem als vollwertiger Ersatz für einen symmetrischen Würfels dienen? Das heißt, kann auch mit einem unsymmetrischen Würfel eine der Zahlen 1 bis 6 zufällig ausgewählt werden, wobei alle sechs Ergebnisse praktisch gleichwahrscheinlich sind?
      Begriffe: Laplace-Modell und dessen Verallgemeinerung
      
   7. Wahrscheinlichkeit und Geometrie
      Angenommen, man wirft in einem Zimmer, dessen Fußboden schlicht aus parallelen Brettern besteht, einen Stab in die Luft und einer der Spieler wettet, daß der Stab keine der Parallelen des Fußbodens kreuzt, während der andere darauf setzt, daß der Stab irgendwelche der Parallelen kreuzt. Man fragt nach der Gewinnaussicht dieser beiden Spieler.
      Begriffe: Buffonsches Nadelproblem, geometrische Wahrscheinlichkeiten
      
   8. Zufall und mathematische Bestimmtheit – unvereinbar?
      Kann die Folge der Dezimalziffern einer Zahl wie beispielsweise der Kreiszahl p = 3,14159265358... genauso zufällig sein wie die Ergebnisse einer Würfelreihe?
      Begriffe: Zufall, axiomatische Wahrscheinlichkeitsrechnung
      
   9. Die Suche nach dem Gleichmöglichen
      In einer amerikanischen Fernsehshow gewinnt der Kandidat der Endrunde ein Auto, wenn er unter drei Türen diejenige errät, hinter der sich ein Auto verbirgt. Hinter jeder der beiden anderen Türen steht – als publikumswirksames Symbol für die Niete – eine Ziege. Um die Spannung zu vergrößern, öffnet der Showmaster nach der Wahl des Kandidaten zunächst eine der beiden verbliebenen Türen. Dabei wählt der Showmaster, der die richtige Tür kennt, immer eine Tür, hinter der eine Ziege steht. Anschließend darf der Kandidat seine getroffene Entscheidung nochmals revidieren und sich für die übrigbleibende dritte Tür unentschieden. Soll er oder soll er nicht?
      Begriffe: gleichmögliche Fälle, bedingte Wahrscheinlichkeit
      
   10. Gewinne im Spiel: Wahrscheinlichkeit und Wert
       Beim Glücksspiel Chuck-a-Luck werden pro Spiel drei Würfel geworfen. Gesetzt werden darf auf eins der sechs Würfelsymbole. Verloren wird, wenn das gesetzte Symbol auf keinem der Würfel erscheint. Andernfalls gewinnt der Spieler zusätzlich zum Einsatz für jeden Würfel, der das gesetzte Symbol zeigt, einen Betrag in Höhe des Einsatzes. Ist die Bank bei Chuck-a-Luck im Vorteil und wenn ja, wie stark?
       Begriffe: Zufallsgröße, Wahrscheinlichkeitsverteilung, Erwartungswert, Varianz, Standardabweichung
       
   11. Welcher Würfel ist der beste?
       Zwei Spieler knobeln darum, wer mit einem Würfel die höchste Zahl erreicht. Gespielt wird mit drei Würfeln, die abweichend vom Standard beschriftet sind. Auf dem ersten Würfel stehen die Zahlen 5-7-8-9-10-18, auf dem zweiten Würfel 2-3-4-15-16-17 und 1-6-11-12-13-14 auf dem dritten. Nacheinander dürfen sich beide Spieler einen Würfel aussuchen. Welchen Würfel sollte der erste Spieler wählen?
       Begriffe: Nicht-Transitivität von Zufallsgrößen
       
   12. Ein Würfel wird getestet
       Ein Würfel, dessen Symmetrie getestet werden soll, wird zehntausendmal geworfen. Als Summe der dabei geworfenen Augenzahlen ergibt sich 37241, das entspricht einem Durchschnitt von 3,7241. Ist eine solche Abweichung vom Idealwert 3,5 unter normalen Umständen möglich? Oder ist das Ergebnis nur dadurch zu erklären, daß der Würfel unsymmetrisch ist?
       Begriffe: Statistik, Hypothese, Test, Stichprobenfunktion, Gesetz der großen Zahlen, Tschebyschewsche Ungleichung
       
   13. Die Normalverteilung: Wie lange braucht man ins Ziel?
       In einem Rennspiel, bei dem es darum geht, die eigene Spielfigur als erster ins Ziel zu würfeln, hat ein Spieler noch 76 Felder vor sich. Pro Zug darf er seine Figur um das Ergebnis zweier Würfel weiterrücken. Wie groß ist die Wahrscheinlichkeit, das Ziel in höchstens neun Zügen zu erreichen?
       Begriffe: zentraler Grenzwertsatz, Normalverteilung
       Spiele: Dampfroß, Risiko, Backgammon
       
   14. Nicht nur beim Roulette: Die Poisson-Verteilung
       Bei 37 Roulette-Läufen ist es kaum zu erwarten, daß alle 37 Zahlen einmal getroffen werden. Wieviel verschiedene Zahlen sind es aber im Durchschnitt?
       Begriffe: Poisson-Verteilung
       
   15. Wenn Formeln zu kompliziert sind: Die Monte-Carlo-Methode
       Zwei Spieler tragen eine Serie von Glücksspielen aus. Gespielt wird jeweils mit einfachem Einsatz. Die Wahrscheinlichkeit, daß der erste Spieler ein Einzelspiel gewinnt, ist 0,52; andernfalls verliert er seinen Einsatz an den Gegner. Zu Beginn verfügt der erste Spieler über ein Kapital von fünf Einsätzen, sein Gegner über 50. Es wird so lange gespielt, bis ein Spieler pleite ist. Wie groß ist die Wahrscheinlichkeit, daß der erste Spieler gewinnt, und wie viele Partien dauert es durchschnittlich bis zum Ruin eines Spielers?
       Begriffe: Monte-Carlo-Methode, Ruin-Problem, Zufallszahlen und ihre Erzeugung
       Spiele: Leiterspiel, Roulette
       
   16. Markow-Ketten und Monopoly
       Beim Spiel Monopoly sollen die Straßenzüge nach den zu erwartenden Mieteinnahmen bewertet werden. Was ist zu tun?
       Begriffe: Markow-Kette
       Spiele: Monopoly, Leiterspiel
       
   17. Black Jack: Ein Märchen aus Las Vegas
       In Spielkasinos gilt Black Jack als das Spiel mit den besten Gewinnchancen. Es wird sogar behauptet, daß es Spielstrategien gebe, bei denen die Chancen des Spielers die der Bank übertreffen. Kann so etwas überhaupt möglich sein?
       Begriffe: Strategie-Optimierung
       Spiele: Black Jack
       
       
2. Kombinatorische Spiele
   1. Welcher Zug ist der beste?
      Beim Schach ist der Zug des weißen Königsbauern e2 - e4 eine gebräuchliche Eröffnung. Schwarz kann unter anderem mit einem der Züge e7 - e5, e7 - e6, c7 - c5 oder Sg8 - f6 antworten. Gibt es unter den vier Zügen zwei, die hinsichtlich der Gewinnaussichten absolut gleichwertig sind?
      Begriffe: Nullsummen-Spiel, perfekte Information, Strategie, Normalform, Zermelos Bestimmtheitssatz
      Spiele: Schach
      
   2. Gewinnaussichten und Symmetrie
      Um keinen Spieler zu begünstigen, sind die Regeln der meisten Brettspiele für beide Spieler annähernd symmetrisch. Wird das Ziel im konkreten Einzelfall aber tatsächlich erreicht?
      Begriffe: Symmetrie, Strategie-Klau, Heiratssatz
      Spiele: Hex, Bridge-it, Tic-Tac-Toe, Mühle
      
   3. Ein Spiel zu dritt
      Von einem Haufen mit anfänglich zehn Steinen nehmen drei Spieler reihum Steine. Jeder Spieler darf pro Zug höchstens fünf Steine nehmen. Derjenige Spieler, der den letzten Stein nimmt, gewinnt eine Einheit und zwar von dem Spieler, der zuvor gezogen hat. Der dritte Spieler geht null auf null aus. Wie verhalten sich die Spieler am besten?
      Begriffe: Gleichgewicht, perfekte Information
      Spiele: Nim
      
   4. Nim: Gewinnen kann ganz einfach sein!
      Zwei Spieler nehmen abwechselnd Steine von drei Haufen, die zu Beginn 6, 7 und 8 Steine umfassen. Pro Zug dürfen nur von einem Haufen Steine genommen werden, allerdings ist die Zahl beliebig. Gewonnen hat der Spieler, der den letzten Stein nimmt. Wie eröffnet man am besten das Spiel?
      Begriffe: Nim-Addition, Verlustposition, Gewinnposition
      Spiele: Nim
      
   5. Lasker-Nim: Gewinn auf verborgenem Weg
      Bei einer Variante des Nim-Spiels entfernt ein Spieler bei seinem Zug entweder Steine von einem Haufen oder er zerlegt einen Haufen mit mindestens zwei Steinen in zwei, nicht unbedingt gleich große Teile. Der Spieler, der den letzten Stein nimmt, gewinnt. Kann man dieses Spiel ähnlich wie Nim auf einfache Weise gewinnen?
      Begriffe: äquivalente Position, disjunktive Summe von Positionen, Grundy-Zahl
      Spiele: Lasker-Nim, Kegel-Nim, Subtraktionspiele, oktale Spiele
      
   6. Schwarz-Weiß-Nim: Jeder zieht mit seinen Steinen
      Schwarz-Weiß-Nim wird mit aus weißen und schwarzen Dame-Steinen aufgebauten Türmen gespielt. Pro Zug wählt ein Spieler einen Stein seiner Farbe aus und entfernt ihn zusammen mit den darüberliegenden Steinen. Der Spieler, dem es gelingt, den letzten Zug zu machen, gewinnt. Wie können Gewinnzüge gefunden werden – beispielsweise für die Position aus Bild 19?

      Bild 19
      Begriffe: kombinatorische Spieltheorie, Conway-Spiele, Conways Zahlbereich-Konstruktionen, Einfachheitssatz
      Spiele: Schwarz-Weiß-Nim
      

   7. Ein Spiel mit Domino-Steinen: Wie lange ist noch Platz?
      Auf einem schachbrettartig eingeteilten Spielfeld legen zwei Spieler abwechselnd Domino-Steine, deren Größe zwei Spielfeldern entspricht. Weiß plaziert seine Steine stets auf zwei bislang unbelegte, senkrecht benachbarte Felder. Schwarz legt seine Steine analog in waagrechter Ausrichtung. Gewonnen hat der Spieler, der den letzten Stein legen kann. Wer kann bei der Position in Bild 24 einen Sieg für sich erzwingen?

      Bild 24
      Begriffe: infinitesimale Spiele, Stop-Werte, Mittelwert, Temperatur, Thermograph
      Spiele: Domino
      

   8. Go: Klassisches Spiel mit moderner Theorie
      Welches sind die besten Züge für Weiß beziehungsweise Schwarz, wenn diese in der Go-Position von Bild 27 am Zuge sind? Wie viele Gewinnpunkte können jeweils erzielt werden?

      Bild 27
      Begriffe: Punktwertungsspiel, mathematisches Go, kaltes Go
      Spiele: Go, Blockbusting
      

   9. Misère-Spiele: Verlieren will gelernt sein!
      Die Regeln von Conway-Spielen lassen sich dahingehend ändern, daß der Spieler, der den letzten Zug macht, nicht gewinnt, sondern verliert. Können für solche umgekehrte Versionen ebenso einfache Kriterien für Gewinnzüge gefunden werden wie das mit Hilfe der Grundy-Zahlen für die normalen Versionen der Fall ist?
      Begriffe: Misère-Spiel, Ausnahmepostion, Sibert-Conway-Zerlegung
      Spiele: Lasker-Nim, Subtraktionsspiele, Kegel-Nim, Nimbi
      
   10. Der Computer als Spielpartner
       Wie denkt ein Schachcomputer?
       Begriffe: Minimax-Algorithmus, Alpha-Beta-Verfahren, Hashing, Endspieldatenbanken
       Spiele: Schach
       
   11. Gewinnaussichten – immer berechenbar?
       Zwei Mathematiker spielen das folgende Spiel: Gezogen wird abwechselnd, wobei sich eine Partie stets über fünf Züge erstreckt. Für jeden Zug denkt sich der betreffende Spieler eine beliebige, nicht negative, ganze Zahl aus und gibt sie seinem Gegner bekannt. Nach fünf Zügen mit den dabei ausgewählten Zahlen x₁, x₂, x₃, x₄, x₅ gewinnt der erste Spieler genau dann, wenn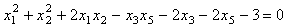

       

       ist. Welcher Spieler besitzt eine Gewinnstrategie?
       Begriffe: Berechenbarkeit, Halteproblem, Zehntes Hilbertsches Problem
       

   12. Spiele und Komplexität: Wenn Berechnungen zu lange dauern
       Gibt es für das Spiel Hex, ähnlich wie es für viele Nim-Varianten der Fall ist, eine "Formel", mit der die Gewinnaussichten schnell berechenbar sind?
       Begriffe: polynomialer Rechenaufwand, NP-harte Probleme
       Spiele: Bridge-it, Hex, Go-Moku, Dame
       
   13. Memory: Gutes Gedächtnis und Glück – sonst nichts?
       Um beim Memory zu gewinnen, benötigt man ein gutes Gedächtnis und ebenso etwas Glück. Gibt es darüber hinaus noch strategische Spielfaktoren, mit denen man seine Gewinnchancen verbessern kann?
       Begriffe: Minimax-Strategie
       Spiele: Memory
       
   14. Backgammon: Doppeln oder nicht?
       Fühlt sich ein Spieler beim Backgammon genügend im Vorteil, darf er den Einsatz verdoppeln. Sein Gegner muß das entweder akzeptieren oder seinen bisherigen Einsatz verloren geben. Natürlich ist ein Spieler, der schlecht steht, kaum an einem Doppel interessiert. Gibt es deshalb überhaupt Doppel, die bei beidseitig fehlerfreiem Spiel zustande kommen?
       Begriffe: Minimax-Algorithmus
       Spiele: Backgammon
       
   15. Mastermind: Auf Nummer sicher
       Wie läßt sich beim Mastermind der gesuchte Code am schnellsten knacken? Wieviele Züge reichen aus, um jeden beliebigen vierstelligen Sechs-Farben-Code sicher entschlüsseln zu können?
       Begriffe: Minimax-Algorithmus
       Spiele: Mastermind
       
       
3. Strategische Spiele
   1. Papier-Stein-Schere: Die unbekannten Pläne des Gegners
      Wollen zwei Personen darum knobeln, wer eine angefallene Zeche zu bezahlen hat, so bietet sich dafür das Spiel Papier-Stein-Schere an. Darin haben beide Spieler übereinstimmende Zug- und Gewinnmöglichkeiten. Anders als bei symmetrischen Zweipersonen-Spielen mit perfekter Information ist aber kein Zug erkennbar, mit dem ein Spieler seinen Verlust verhindern kann. Was ist zu tun?
      Begriffe: imperfekte Information, gemischte Strategie
      Spiele: Papier-Stein-Schere
      
   2. Minimax kontra Psychologie: Selbst beim Pokern?
      Zwei Spieler pokern eine Runde von zwei Partien, bei denen das Eröffnungsrecht abwechselt. Kann ein Spieler seine Strategie zufallsabhängig so variieren, daß er in einen durchschnittlichen Gesamtverlust verhindern kann?
      Begriffe: Minimax-Satz
      Spiele: Poker
      
   3. Poker-Bluff: Auch ohne Psychologie?
      Der Erfolg eines guten Pokerspielers beruht zum Teil auf seinen Bluffs. Auf welcher Basis entscheidet man sich aber zu einem solchen Bluff? Setzen Bluffs eine treffende psychologische Einschätzung des Gegners voraus? Oder sind sie Ausdruck einer objektiven Optimalität im mathematischen Sinn, mit der die strategischen Möglichkeiten des Gegners Minimax-mäßig pariert werden?
      Begriffe: Minimax-Strategie
      Spiele: Pokern
      
   4. Symmetrische Spiele: Nachteile sind vermeidbar, aber wie?
      Bei symmetrischen Zwei-Personen-Nullsummenspiele ist beiden Spielern die Existenz einer gemischten Strategie garantiert, mit der eine negative Gewinnerwartung verhindert werden kann. Wie läßt sich eine solche Strategie berechnen?
      Begriffe: lineare Ungleichungssysteme, Lineare Optimierung, Simplex-Algorithmus
      
   5. Minimax und Lineare Optimierung: So einfach wie möglich
      Gesucht ist eine möglichst einfache Methode, mit der Minimax-Strategien für beide Spieler eines als Normalform gegebenen Zwei-Personen-Nullsummenspiels berechnet werden können.
      Begriffe: Simplex-Algorithmus, duale Probleme,
      
   6. Play it again: Aus Erfahrung klug?
      Reicht allein Erfahrung im Spiel dazu aus, gute Spielstrategien zu finden? Konkret: Läßt sich zu jedem gegebenen Zwei-Personen-Nullsummenspiel eine Serie von Partien organisieren, mit der Minimax-Strategien empirisch bestimmt werden können?
      Begriffe: Iteration auf Basis einer Partienserie
      
   7. Le Her: Tauschen oder nicht?
      Weiß und Schwarz spielen darum, wer die höhere Karte erlangt. Gespielt wird mit einem normalen 52er-Blatt, für das die Rangfolge König, Dame, Bube, 10, 9, ... 3, 2, As gilt. Bei gleich hohen Kartenwerten gewinnt Schwarz.

      Zu Beginn erhält jeder Spieler eine Karte, und eine weitere wird verdeckt auf den Tisch gelegt. Anschließend bekommt jeder Spieler eine Chance, seinen Kartenwert zu verbessern. Weiß beginnt und darf dabei den Austausch seiner Karte mit Schwarz verlangen. Sofern Schwarz keinen König auf der Hand hält, muß er sich einem gewünschten Tausch fügen. Unabhängig davon, wie die erste Tauschmöglichkeit verlaufen ist, erhält nun Schwarz seine Chance: Dabei darf er seine Karte mit der verdeckt auf dem Tisch liegenden Karte tauschen, wobei auch er einen König zurücklegen muß. Anschließend legen die beiden Spieler ihre Karten auf den Tisch und rechnen ab.

      Welche Karten sollten die Spieler tauschen und welche nicht?
      Begriffe: Strategie-Auswahl, relative Minimax-Strategie, optimale Gegenstrategie
      Spiele: Ler Her

   8. Zufällig entscheiden – aber wie?
      Ein Spieler realisiert eine gemischte Strategie, indem er zu Beginn einer Partie eine einzige Zufallsentscheidung darüber herbeiführt, die sein gesamtes Verhalten innerhalb der nachfolgenden Partie festlegt. Kann das zufällige Spielerverhalten einer Minimax-Strategie auch Zug für Zug organisiert werden? Das heißt, läßt sich jeder anstehende Zug durch eine separate Zufallsentscheidung ermitteln?
      Begriffe: Verhaltensstragie, perfektes Erinnerungsvermögen
      Spiele: Pokern
      
   9. Optimal handeln – effizient geplant
      Bei Zwei-Personen-Nullsummenspielen mit perfektem Erinnerungsvermögen lassen sich Minimax-Strategien in Form von Verhaltensstrategien zumindest dann einfach beschreiben, wenn die Anzahl der möglichen Informationsmengen nicht zu groß ist. Der zur Berechnung notwendige Aufwand kann aber erheblich sein. In welchem Maße ist er begrenzbar?
      Begriffe: Realisierungsgewicht, Realisierungsplan
      Spiele: Pokern
      
   10. Baccarat: Ziehen bei Fünf?
       Sollte ein Baccarat-Spieler, der mit seinen ersten beiden Karten den Wert Fünf erzielt, eine weitere Karte verlangen?
       Begriffe: Minimax-Strategie
       Spiele: Baccarat
       
   11. Pokern zu dritt: Vertrauenssache?
       Drei Spieler pokern gegeneinander. Können zwei Spieler ihre Spielweise zum Schaden des dritten aufeinander abstimmen, ohne dabei zu mogeln?
       Begriffe: nicht kooperative Spieltheorie, Nash-Gleichgewicht, kooperative Spieltheorie, Koalition
       Spiele: Pokern
       
   12. "QUAAK!" – (k)ein Kinderspiel
       Zwei Spieler knobeln nach den folgenden Regeln: Zu Beginn erhalten beide Spieler je 15 Chips, mit denen sie mehrere Runden austragen. Pro Runde nimmt jeder Spieler eine bestimmte Zahl seiner ihm noch verbliebenen Chips – zulässig ist jede Zahl zwischen 0 und 3 – in seine geschlossene Hand. Nachdem beide Spieler ihre Wahl geheim getroffen haben, öffnen sie ihre Hand und vergleichen. Hat ein Spieler mehr Chips in seiner Hand als sein Gegner, erhält er einen Punkt. Nach der Runde werden die gesetzten Chips beider Spieler weggelegt. Ein Spieler gewinnt, wenn es im gelingt, drei Punkte mehr als sein Gegner zu erlangen; ansonsten endet das Spiel unentschieden. Wie verhält man sich am besten?
       Begriffe: Minimax-Strategie
       Spiele: QUAAK!
       

   13. Mastermind: Farbcodes und Minimax
       In wieweit kann beim Mastermind der den Farbode vorgebende "Codierer" die Gewinnaussichten des Spiels beeinflussen?
       Begriffe: Minimax-Strategie, Symmetrie
       Spiele: Mastermind

Die grau unterlegten Tabellenzeilen sind ab der 2. Auflage, die gelb hinterlegten Tabellenzeilen ab der 3. Auflage berücksichtigt.

---

Weitere Dokumente:

English version
(only preface and contents as PDF file):
Luck, Logic and Whie Lies:
The Mathematics of Games

Games in the View of Mathematics
Sheets of a talk

PDF-Version
(nur Einführung und Inhaltsverzeichnis):
Glück, Logik Bluff:
Mathematik im Spiel - Methoden, Ergebnisse und Grenzen

Die Analyse von (Bei-)Spielen
Folien zu einem Vortrag zum Thema
"Gesellschaftsspiele und Spieltheorie"

Die Mathematik der Gesellschaftsspiele
Vortragsfolien

Spiele aus mathematischer Sicht (garantiert ohne Formeln)
Vortragsfolien und Manuskript

Go und Mathematik:
Eine Anwendung der kombinatorischen Spieltheorie


Ergänzungen zum Buch:

Monopoly und Mathematik:
Interaktive Demos

Black Jack und Mathematik:
JavaScript-basierter Strategie-Optimierer

Der Computer, der sich nicht bluffen lässt:
Optimales Spielen dank Spieltheorie


Beiträge zu anderen Themen:

Die Ideen der Galois-Theorie